-
Max
Starting from either exponential version of max:
;; max : non-empty-list-of-numbers 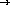 number
(define (max alon)
(cond
[(null? (cdr alon)) (first alon)]
[else (cond
[(< (car alon) (max (cdr alon)))
(max (cdr alon))]
[else
(car alon)])]))
;; max : list-of-positive-numbers
number
(define (max alon)
(cond
[(null? (cdr alon)) (first alon)]
[else (cond
[(< (car alon) (max (cdr alon)))
(max (cdr alon))]
[else
(car alon)])]))
;; max : list-of-positive-numbers 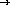 number
(define (max alon)
(cond
[(null? alon) 0]
[else (cond
[(< (car alon) (max (car alon)))
(max (cdr alon))]
[else
(car alon)])]))
number
(define (max alon)
(cond
[(null? alon) 0]
[else (cond
[(< (car alon) (max (car alon)))
(max (cdr alon))]
[else
(car alon)])]))
use let to formulate an alternate version of that
only uses a linear number of recursive calls.
Solution
;; max : non-empty list of numbers 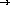 number
(define (max alon)
(cond
[(null? (cdr alon)) (car alon)]
[else (let ([rst (max (cdr alon))])
(cond
[(< (car alon) rst)
rst]
[else
(car alon)]))]))
;; max : list of positive numbers
number
(define (max alon)
(cond
[(null? (cdr alon)) (car alon)]
[else (let ([rst (max (cdr alon))])
(cond
[(< (car alon) rst)
rst]
[else
(car alon)]))]))
;; max : list of positive numbers 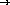 number
(define (max alon)
(cond
[(null? alon) 0]
[else (let ([rst (max (cdr alon))])
(cond
[(< (car alon) rst)
rst]
[else
(car alon)]))]))
number
(define (max alon)
(cond
[(null? alon) 0]
[else (let ([rst (max (cdr alon))])
(cond
[(< (car alon) rst)
rst]
[else
(car alon)]))]))
-
Best
Abstract over the comparison operator in max and
produce a function best that accepts a function
and returns the best element, according to that function.
Here's the header and purpose statement for best:
;; best : (integer integer 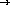 boolean) list-of-numbers
boolean) list-of-numbers 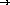 number
(define (best metric a-lon)
...)
number
(define (best metric a-lon)
...)
Solution
(define (best metric a-lon)
(cond
[(null? a-lon) 0]
[else (let ([rst (best metric (cdr a-lon))])
(if (metric (car a-lon) rst)
(car a-lon)
rst))]))
Write both max and min in terms of
best.
Solution
(define (max l) (best >= l))
(define (min l) (best <= l))
-
Filter
Write a function called filter-lt7 that returns
all of the elements in a list that are less than
7.
Solution
;; filter-lt7 : list-of-numbers 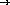 list-of-numbers
(define (filter-lt7 a-lon)
(cond
[(null? a-lon) '()]
[else (if (<= (car a-lon) 7)
(cons (car a-lon) (filter-lt7 (cdr a-lon)))
(filter-lt7 (cdr a-lon)))]))
list-of-numbers
(define (filter-lt7 a-lon)
(cond
[(null? a-lon) '()]
[else (if (<= (car a-lon) 7)
(cons (car a-lon) (filter-lt7 (cdr a-lon)))
(filter-lt7 (cdr a-lon)))]))
Write the function filter that accepts a predicate
on numbers and returns all of the elements in the list that
satisfy the predicate. Here is the header and purpose
statement for the function:
;; filter : (number 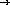 boolean) list-of-numbers
boolean) list-of-numbers 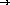 list-of-numbers
(define (filter p a-lon)
...)
list-of-numbers
(define (filter p a-lon)
...)
Solution
;; filter : (number 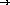 boolean) list-of-numbers
boolean) list-of-numbers 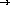 list-of-numbers
(define (filter p a-lon)
(cond
[(null? a-lon) '()]
[else (if (p (car a-lon))
(cons (car a-lon) (filter p (cdr a-lon)))
(filter p (cdr a-lon)))]))
list-of-numbers
(define (filter p a-lon)
(cond
[(null? a-lon) '()]
[else (if (p (car a-lon))
(cons (car a-lon) (filter p (cdr a-lon)))
(filter p (cdr a-lon)))]))
Using filter, re-define filter-lt7. Also,
define filter-odd, a function that accepts a list
and returns a list containing the odd numbers in its input.
Solution
(define (filter-lt7 l)
(filter (lambda (x) (<= x 7)) l))
(define (filter-odd l)
(filter odd? l))
-
Building Lists
Define a function called build-consecutive-list
that accepts a number and returns a list of the number
from that number down to 1.
Solution
;; build-consecutive-list : number 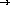 (listof numbers)
(define (build-consecutive-list n)
(cond
[(zero? n) '()]
[else
(cons n (build-consecutive-list (- n 1)))]))
(listof numbers)
(define (build-consecutive-list n)
(cond
[(zero? n) '()]
[else
(cons n (build-consecutive-list (- n 1)))]))
Define a function called build-list that accepts a
number n and a function f from numbers to
numbers and returns a list consisting of the results of
calling f on the numbers from n down to
1.
Solution
;; build-list : number 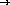 (listof numbers)
(define (build-list f n)
(cond
[(zero? n) '()]
[else
(cons (f n) (build-list f (- n 1)))]))
(listof numbers)
(define (build-list f n)
(cond
[(zero? n) '()]
[else
(cons (f n) (build-list f (- n 1)))]))
Use build-list to redefine
build-consecutive-list and to define
build-perect-squares, a function that returns
the first n perfect squares.
Solution
(define (build-consecutive-list l)
(build-list (lambda (x) x) l))
(define (build-perfect-squares l)
(build-list (lambda (x) (* x x)) l))
-
Binding Structure
Draw arrows to indicate the binding structure of these
programs [note: DrScheme's Check Syntax will tell you the
answers to this question, but you will not have Check
Syntax available to you on the exam. Be sure you can
figure these out by yourself]:
(define (f x)
x)
(f 1)
(define (len l)
(cond
[(null? l) 0]
[else (+ (len (cdr l)) 1)]))
(define (quad x)
(let ([sq (* x x)])
(* sq sq)))
(define (g x)
(let ([x x])
(+ x x)))
(define (g x)
(let ([x x]
[y x])
(+ x x)))
Solution
Use Check Syntax in DrScheme.