Family Trees
Recall the data definition for family trees:
A family-tree is either:
(define-struct ft (name eye-color mom dad))
Write a function called path-to-blue-eyes that
finds a path to a blue-eyed ancestor, if one exists and
returns #f if there aren't any. A path is
represented as a list of symbols, either 'mom or
'dad.
Here are some examples (be sure to use these as tests when
developing your function):
(define tutu (make-ft 'emily 'brown 'unknown 'unknown))
(define opa (make-ft 'bruce 'blue 'unknown 'unknown))
(define mom (make-ft 'alice 'green tutu opa))
(define dad (make-ft 'bill 'brown 'unknown 'unknown))
(define me (make-ft 'robby 'hazel mom dad))
(path-to-blue-eyes 'unknown) "should be" #f
(path-to-blue-eyes tutu) "should be" #f
(path-to-blue-eyes opa) "should be" '()
(path-to-blue-eyes mom) "should be" '(dad)
(path-to-blue-eyes dad) "should be" #f
(path-to-blue-eyes me) "should be" '(mom dad)
Solution
There is more than one solution to this problem, since
there may be more than one path to a blue eyed ancestor
and different functions may find different paths. Here's
one solution:
;; path-to-blue-eyes : family-tree 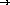 list-of-symbols or #f
(define (path-to-blue-eyes ft)
(cond
[(eq? ft 'unknown) #f]
[else
(if (eq? (ft-eye-color ft) 'blue)
'()
(let ([mom-path (path-to-blue-eyes (ft-mom ft))]
[dad-path (path-to-blue-eyes (ft-dad ft))])
(cond
[(and mom-path dad-path) (cons 'mom mom-path)]
[(and mom-path (not dad-path)) (cons 'mom mom-path)]
[(and dad-path (not mom-path)) (cons 'dad dad-path)]
[else #f])))]))
list-of-symbols or #f
(define (path-to-blue-eyes ft)
(cond
[(eq? ft 'unknown) #f]
[else
(if (eq? (ft-eye-color ft) 'blue)
'()
(let ([mom-path (path-to-blue-eyes (ft-mom ft))]
[dad-path (path-to-blue-eyes (ft-dad ft))])
(cond
[(and mom-path dad-path) (cons 'mom mom-path)]
[(and mom-path (not dad-path)) (cons 'mom mom-path)]
[(and dad-path (not mom-path)) (cons 'dad dad-path)]
[else #f])))]))
Sets
Write a function called union that computes the
union of two sets. The union of two sets is a set that
contains all of the elements in both sets.
Write your data definition for sets, along with any
invariants of the data definition and be sure that your
function satisfies those invariants.
Here is a function header for union
;; union : set-of-numbers set-of-numbers 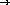 set-of-numbers
(define (union s1 s2)
...)
set-of-numbers
(define (union s1 s2)
...)
Solution
Here are two possible solutions:
A set-of-numbers is either:
Invariant: the set of numbers does not contain any duplicates.
;; union : set-of-numbers 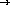 set-of-numbers
(define (union s1 s2)
(cond
[(null? s1) s2]
[else (let ([un (union (cdr s1) s2)])
(if (number-in-set? (car s1) un)
un
(cons (car s1) un)))]))
;; number-in-set? number set-of-numbers
set-of-numbers
(define (union s1 s2)
(cond
[(null? s1) s2]
[else (let ([un (union (cdr s1) s2)])
(if (number-in-set? (car s1) un)
un
(cons (car s1) un)))]))
;; number-in-set? number set-of-numbers 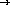 boolean
(define (number-in-set? num set)
(cond
[(null? set) #f]
[else (or (= num (car set))
(number-in-set? num (cdr set)))]))
boolean
(define (number-in-set? num set)
(cond
[(null? set) #f]
[else (or (= num (car set))
(number-in-set? num (cdr set)))]))
A set-of-numbers is either:
Invariant: the set of numbers is in sorted order and does
not contain any duplicates.
This function processes two complex forms of data
simultaneously:
;; union : set-of-numbers 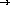 set-of-numbers
(define (union s1 s2)
(cond
[(and (null? s1) (null? s2)) '()]
[(null? s1) s2]
[(null? s2) s1]
[else (let ([fst-s1 (car s1)]
[fst-s2 (car s2)])
(cond
[(= fst-s1 fst-s2)
(cons fst-s1 (union (cdr s1) (cdr s2)))]
[(< fst-s1 fst-s2)
(cons fst-s1 (union (cdr s1) s2))]
[(< fst-s2 fst-s1)
(cons fst-s2 (union s1 (cdr s2)))]))]))
set-of-numbers
(define (union s1 s2)
(cond
[(and (null? s1) (null? s2)) '()]
[(null? s1) s2]
[(null? s2) s1]
[else (let ([fst-s1 (car s1)]
[fst-s2 (car s2)])
(cond
[(= fst-s1 fst-s2)
(cons fst-s1 (union (cdr s1) (cdr s2)))]
[(< fst-s1 fst-s2)
(cons fst-s1 (union (cdr s1) s2))]
[(< fst-s2 fst-s1)
(cons fst-s2 (union s1 (cdr s2)))]))]))