Homework is no longer required. Do it for more practice on the topics covered in lecture. Email it to yuhu@cs.uchicago.edu and put your name and the homework number in the Subject line of your message if you want to get feedback on it.All assignment numbers come from the online version of the text.They may be slightly different in the first and second printing (but they match the third printing). |
| Due Date | Language (in DrScheme) | Problems |
|---|
| 11/17 | Intermediate Student w/lambda | Write the function:
;; same-graph? : (graph X) (graph X) -> boolean
;; to determine g1 and g2 have the same nodes,
;; and each node in g1 has the same neighbors as that node in g2.
;; assume that both graphs have the same node equality function.
(define (same-graph? g1 g2) ...)
;; examples as tests
(same-graph? (make-graph '() (lambda (x) '()) symbol=?)
(make-graph '() (lambda (x) '()) symbol=?))
true
(same-graph? (make-graph '(a) (lambda (x) '()) symbol=?)
(make-graph '() (lambda (x) '()) symbol=?))
false
(same-graph? (make-graph '(a) (lambda (x) '()) symbol=?)
(make-graph '(a) (lambda (x) '()) symbol=?))
true
(same-graph? (make-graph '(b) (lambda (x) '()) symbol=?)
(make-graph '(a) (lambda (x) '()) symbol=?))
false
(same-graph? (make-graph '(a b) (lambda (x) '()) symbol=?)
(make-graph '(b a) (lambda (x) '()) symbol=?))
true
(same-graph? (make-graph '(a b)
(lambda (x)
(cond
[(symbol=? x 'a) '(b)]
[(symbol=? x 'b) '()]))
symbol=?)
(make-graph '(a b)
(lambda (x)
(cond
[(symbol=? x 'b) '(a)]
[(symbol=? x 'a) '()]))
symbol=?))
false
(same-graph? (make-graph '(a b)
(lambda (x)
(cond
[(symbol=? x 'a) '(a b)]
[(symbol=? x 'b) '()]))
symbol=?)
(make-graph '(a b)
(lambda (x)
(cond
[(symbol=? x 'a) '(b a)]
[(symbol=? x 'b) '()]))
symbol=?))
true
Write the following two functions and use same-graph? to test them.
;; reverse-edge-graph : (graph X) -> (graph X)
;; to build a graph with the same nodes as g, but with reversed edges.
;; that is, if g has an edge from a to b then the result graph will have an edge from b to a.
(define (reverse-edge-graph g) ...)
;; undirected? : (graph X) -> boolean
;; to determine if each edge in g has a matching edge going the opposite direction
(define (undirected? g) ...)
Write the following functions using an accumulator.
;; posn-sum : (listof posn) -> posn
;; compute a posn whose x coordinate is the sum of the x coordinates in ps
;; and whose y coordinates is the sum of the y coordinates in ps
(define (posn-sum ps) ...)
;; digits->num : (listof digit) -> number
;; to compute the number represented by the list of digits
(define (digits->num ds) ...)
;; examples as tests:
(digits->num (list 1 2 3))
123
(digits->num empty)
0
Using this data definition for a family tree, define the function below using an accumulator.
;; a family-tree is either:
;; - empty
;; - (make-node symbol family-tree family-tree)
(define-struct node (name mom dad))
;; second? : family-tree -> boolean
;; to determine if any child has the same name as an ancestor of theirs.
(define (second? ft) ...)
|
| 11/15 | Intermediate Student w/lambda | Revisit the function reverse from earlier in class. It takes a list of numbers and returns the same list, but in the reverse order. Write it out (following the design recipe as you did before.)
This function suffers from the same flaw as the food-chain function in lecture. Rewrite it using an accumulator to fix the problem. Re-use your tests from above to make sure it still is right.
Write the product function using an accumulator (it takes a list of numbers and returns their product). |
| 11/13 | Intermediate Student w/lambda | Implement find-paths.
; a (graph X) is:
; (make-graph (listof X) (X -> (listof X) (X X -> boolean))
(define-struct graph (nodes neighbors node-equal?))
; find-paths : (graph X) X X -> (listof (listof X))
; to find all of the paths in the graph from src to dest
(define (find-paths graph src dest) ...)
|
| 11/10 | Intermediate Student w/lambda | HtDP 26.3.1, 26.3.2, 26.3.3, 26.3.4 |
| 11/8 | Intermediate Student w/lambda | HtDP: 25.2.2, 25.2.3, 25.2.4, 25.2.6
For 25.2.3, use (time ...) to determine what the cutoff should be before switching from quick-sort to sort. For example, (time (quick-sort (forge-list 100 (lambda (x) (random 1000))))) tells you how long quick-sort takes to sort a list of 100 random numbers. |
| 11/6 | Intermediate Student w/lambda | Write the following functions. You may not use +, * or expt.
;; add : nat nat -> nat
;; to add the two nats together
;; mul : nat nat -> nat
;; to multiply the two nats together
;; pow : nat nat -> nat
;; to compute x to the n-th power
(define (pow x n) ...)
;; forge-list : nat (nat -> X) -> (listof X)
;; to forge a list of length N where the
;; last element is (f 0), the second to last is (f 1), etc
(define (forge-list n f) ...)
;; examples as tests
(forge-list 4 (lambda (x) x))
(list 3 2 1 0)
;; triangular-list : nat -> (listof (listof 'x))
;; to build a triangular list of lists of the symbol 'x
(define (triangular-list i) ...)
;; examples as tests
(triangular-list 4)
(list (list 'x) (list 'x 'x) (list 'x 'x 'x) (list 'x 'x 'x 'x)) |
| 11/3 | Intermediate Student w/lambda | a) Hand evaluate: (show all steps)
(define mul (lambda (x) (lambda (y) (* x y))))
(define m3 (mul 3))
(+ (m3 3) (m3 4))
b) Hand evaluate: (show only recursive calls)
(map (lambda (x) (expt x 3)) (list 1 2 3))
b) Hand evaluate: (show only recursive calls)
(filter (lambda (x) (zero? (modulo x 3))) (list 5 6 7))
If you don't know what some of the primitives above do, try them out in the interactions window. |
| 11/1 | Intermediate Student | Do not write any recursive functions for this homework.
map, filter, and foldr are built in to DrScheme.
Use map to write the next function.
;; build-straight-line : num (listof num) -> (listof posn)
;; returns a list of posns where the X coordinate is n and
;; the Y coordinate is a number
;; in lon
;; e.g., (build-straight-line 2 (list 1 2 3))
;; (list (make-posn 2 1) (make-posn 2 2) (make-posn 2 3))
(define (build-straight-line n lon) ...)
Use filter to write the next function.
;; pts-north : posn (listof posn) -> (listof posn)
;; returns the posns from lop that are north of p,
;; that is, whose y coordinate is greater than p's y coordinate
(define (pts-north p lop) ...)
Use foldr to write the next function.
;; total-width : (listof image) -> num
;; returns the sum of the widths of all images in loi
(define (total-width loi) ...)
Use map filter and foldr to write the next four functions.
The next exercises use functions to represent curves in the plane. A curve can be represented as a function that accepts an x coordinate and returns a y coordinate. For example, the straight line through the origin can be represented as
(define (diagonal x) x)
and a parabola sitting on the origin can be represented as
(define (parabola x) (* x x))
(define points (list (make-posn 1 0) (make-posn 1 1) (make-posn 2 2)))
;; points-on-line : (num -> num) (listof posn) -> (listof posn)
;; return the points in pts that are on the curve described by f
;; e.g.
;; (points-on-line diagonal points) 'shouldbe (list (make-posn 1 1) (make-posn 2 2))
;; (points-on-line parabola points) 'shouldbe (list (make-posn 1 1))
(define (points-on-line f pts) ...)
;; positions: (num -> num) (listof num) -> (listof posn)
;; returns a list of positions on the curve `f' whose x-coordinates
;; are in lon
;; e.g., (positions parabola (list 1 2 3))
;; (list (make-posn 1 1) (make-posn 2 4) (make-posn 3 9))
(define (positions f lon) ...)
;; flatten-posns : (listof posn) -> (listof num)
;; constructs the list consisting of all the X and Y coordinates of each
;; of the posns in lop, in order.
;; e.g., (flatten-posns points) 'shouldbe (list 1 0 1 1 2 2)
(define (flatten-posns lop) ...)
;; possible-y-coords : (listof (num -> num)) num -> (listof num)
;; given a list of lines lof and an x-coordinate, returns the list
;; of what y-coordinate is associated with that x-coordinate in each curve
;; e.g. (possible-y-coords (list diagonal parabola) 7)
;; (list 7 49)
(define (possible-y-coords lof x) ...)
|
| 10/30 | Intermediate Student | Write best-image:
; best-image : (image image -> boolean) non-empty-list-of-images -> image
; to find the best image in a non-empty list of images,
; where pred indicates if one image is better than another
(define (best-image pred a-neloi) ...)
Use best-image to re-define the two functions that were due on 10/23. |
| 10/27 | Intermediate Student | HtDP: 15.1.2, 15.1.3, and 15.1.4 |
| 10/23 | Intermediate Student | For this assignment, you must not duplicate any recursive calls,
and if you write any helper functions, enclose them in a local.
Consider the data definition and template for non-empty list of images:
; a non-empty-list-of-images is either
; - (cons image empty)
; - (cons image non-empty-list-of-images)
;; neloi-template : non-empty-list-of-imges -> ???
(define (neloi-template a-neloi)
(cond
[(empty? (rest a-neloi)) ... (first a-neloi) ...]
[else ... (first a-neloi) ...
... (neloi-template (rest a-neloi)) ...]))
; narrowest-image : non-empty-list-of-images -> image
; to find the image with the smallest width
; darkest-image : non-empty-list-of-images -> image
; to find the image with the lowest average color component
; (considering all three color components in each color)
|
| 10/20 | Beginning Student w/List Abbreviations | Write the functions:
; sum-pairs : list-of-numbers list-of-numbers -> list-of-numbers
; produces a list of the pairwise sums of the numbers in alon1 and alon2
(define (sum-pairs a-lon1 alon2) ...)
; examples as tests
(sum-pairs empty empty) = empty
(sum-pairs (list 1 3 5) (list 9 17 2001)) = (list 10 20 2006)
; all-in : list-of-numbers list-of-numbers -> boolean
; determines if all of the numbers in alon1 are in alon2
(define (all-in alon1 alon2) ...)
; examples as tests
(all-in empty empty) = true
(all-in (list 1) empty) = false
(all-in empty (list 1)) = true
(all-in (list 1) (list 3 1 4)) = true
(all-in (list 3 1 4) (list 3)) = false
|
| 10/18 | Beginning Student w/List Abbreviations | HtDP: 14.2.3, 14.2.5, 14.2.6 |
| 10/16 | Beginning Student w/List Abbreviations | Write the following functions.
;; above : image image -> image
;; to put one image above another
;; HINT: use put-pinhole to move the pinhole of
;; the first to the middle of the bottom edge
;; and the second to the middle of the top edge
(define (above i1 i2) ...)
;; a lego is
;; - (make-lego symbol number)
(define-struct lego (color width))
;; lego->image : lego -> image
;; to render a lego brick. All legos are rectangular
;; and are 10 pixels tall
(define (lego->image l) ...)
;; a lego-building is either:
;; - lego
;; - (make-bigger lego lego-building lego-building)
(define-struct bigger (lego left right))
;; how-high : lego-building -> number
;; to determine how high a lego building is, in pixels
;; (reminder: each lego is ten pixels tall)
(define (how-high an-lb) ...)
;; find-colored-brick : lego-building color -> lego or false
;; to find any colored brick with the color `color' in an-lb
;; or return false if there are no such legos.
(define (find-colored-brick an-lb color) ...)
;; lb->image : lego-building -> image
;; to render a lego building into an image
(define (lb->image an-lb) ...)
;; Examples as tests
;; (make more tests yourself -- these should be your last tests!)
(lb->image
(make-bigger (make-lego 'blue 100)
(make-bigger (make-lego 'green 60)
(make-lego 'orange 40)
(make-lego 'purple 40))
(make-bigger (make-lego 'pink 60)
(make-lego 'orange 40)
(make-lego 'purple 40))))

(lb->image
(make-bigger (make-lego 'lightblue 80)
(make-bigger (make-lego 'blue 40)
(make-bigger (make-lego 'green 20)
(make-lego 'orange 10)
(make-lego 'purple 10))
(make-bigger (make-lego 'pink 20)
(make-lego 'orange 10)
(make-lego 'purple 10)))
(make-bigger (make-lego 'salmon 40)
(make-bigger (make-lego 'green 20)
(make-lego 'orange 10)
(make-lego 'purple 10))
(make-bigger (make-lego 'pink 20)
(make-lego 'orange 10)
(make-lego 'purple 10)))))
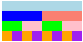 |
| 10/13 | Beginning Student w/List Abbreviations | Write the following functions.
; a ftn is either
; - 'unknown, or
; - (make-child symbol number symbol ftn ftn)
(define-struct child (name date eyes mom dad))
; 40-year-old-ancestor? : ftn -> boolean
; to determine if a 40-year-old ancestor is in a-ftn
(define (40-year-old-ancestor? a-ftn) ...)
; count : ftn -> number
; to count the number of people in a-ftn
(define (count a-ftn) ...)
; avg-age : ftn -> number
; to determine the average age in an-ftn
(define (avg-age a-ftn) ...)
Hint: use helper functions
|
| 10/11 | Beginning Student w/List Abbreviations | Use the web-itunes teachpack for this exercise.
;; render-albums : list-of-album -> html
;; build a web page like we did in class, but include
;; all of the songs with each album, in a table inside a table.
(define (render-albums an-loa) ...)
Use this expression
(save-web-page "index.html" "Robby's Music" robbys-itunes)
to test your functions on some large inputs.
Hint: only do this when you have tested all of your functions carefully with small inputs! |
| 10/9 | Beginning Student | ; sq-nums : list-of-numbers -> list-of-numbers
; to square each element in alon
(define (sq-nums alon) ...)
; rev : list-of-numbers -> list-of-numbers
; to reverse the elements in alon
(define (rev alon) ...)
Hint: break down complex tasks into smaller ones. Wishlists!
Images: 4.1 - 4.3 |
| 10/6 | Beginning Student | Write the following functions. Don't forget about re-use and helper functions (the functions we wrote in class are fair game for re-use as helper functions).
; a list-of-symbols is either
; - empty, or
; - (cons symbol list-of-symbols)
; contains-doll? : list-of-symbols -> boolean
; to determine if 'doll appears in alos
(define (contains-doll? alos) ...)
; a list-of-numbers is either
; - empty, or
; - (cons number list-of-numbers)
; len : list-of-numbers -> number
; to determine the number of elements in alon
(define (len alon) ...)
; avg : list-of-numbers -> number
; to determine the average of the elements in alon
(define (avg alon) ...) |
| 10/4 | Beginning Student | HtDP: 7.2.2 (make sure all vehicles have wheels)
Develop the function toll : vehicle -> number. It determines the amount a vehicle must pay at a toll. The toll costs $0.50 per wheel.
Extend the animal data definition from class with one new kind of animal. Make sure the new animal has a weight.
Write a template for the extended animal data definition.
Write the function diet : animal -> animal. It accepts an animal and returns the same animal, but with half of the weight. |
| 10/2 | Beginning Student | Write the function direct-to-0 : posn -> number that determines how far a posn is from the origin, as the crow flies.
Write the function downtown-to-0 : posn -> number that determines how far a posn is from the origin, if the coordinates were block numbers in downtown Chicago. That is, you cannot cut through buildings and have to walk on streets (this is commonly called "Manhattan" distance, but we know better).
Write the function direct-between : posn posn -> number that determines the distance between two points, as the crow flies. (Hint: wishlists & reuse!)
Images: 3.1 - 3.2 |
| 9/29 | Beginning Student | Images: 2.1 - 2.3 |
| 9/27 | Beginning Student | Images: 1.1 - 1.5 |

