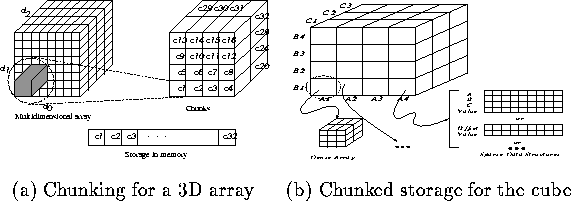
Multidimensional database technology facilitates flexible, high performance access and analysis of large volumes of complex and interrelated data [Sof97]. It is more natural and intuitive for humans to model a multidimensional structure. A chunk is defined as a block of data from the multidimensional array which contains data in all dimensions. A collection of chunks defines the entire array. Figure 1(a) shows chunking of a three dimensional array. A chunk is stored contiguously in memory and data in each dimension is strided with the dimension sizes of the chunk. Most sparse data may not be uniformly sparse. Dense clusters of data can be stored as multidimensional arrays. Sparse data structures are needed to store the sparse portions of data. These chunks can then either be stored as dense arrays or stored using an appropriate sparse data structure as illustrated in Figure 1(b). Chunks also act as an index structure which helps in extracting data for queries and OLAP operations.
Figure 1: Storage of data in chunks
Typically, sparse structures have been used for advantages they provide
in terms of storage, but operations on data are performed on a
multidimensional array which is populated from the sparse
data. However, this is not always possible when either the dimension
sizes are large or the number of dimensions is large. Since we are
dealing with multidimensional structures for a large number of
dimensions, we are interested in performing operations on the sparse
structure itself. This is desirable to reduce I/O costs by having more
data in memory to work on. This is one of the primary motivations for
our Bit-encoded sparse storage (BESS). For each cell present in a
chunk a dimension index is encoded in 
bits
for each dimension 
of size 
. A 8-byte encoding is used to
store the BESS index along with the value at that location. A larger
encoding can be used if the number of dimensions are larger than 20.
A dimension index can
then be extracted by a bit mask operation. Aggregation along a
dimension can be done by masking its dimension encoding in BESS
and using a sort operation to get the duplicate resultant BESS values
together. This is followed by a scan of the BESS index, aggregating values
for each duplicate BESS index. For dimensional analysis, aggregation needs to
be done for appropriate chunks along a dimensional plane.