In a full data cube, the number of aggregates is exponential. In the
cube lattice there are n levels and for each level i there are
aggregates at
each level containing i dimensions. The total number of aggregates,
thus is 
. For a large number of dimensions, this leads to a
prohibitively large number of cubes to materialize.
Next, we need to determine the number of intermediate aggregates needed to calculate all the aggregates for all levels below a specified m, m < n, for m-way associations and for meta-rules with m predicates.
For m=2, the number of aggregates at
level 2 is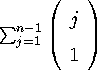 
. For level 3 it is 
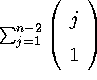. At each level k, the
first k-1 literals in the representation are fixed and the others
are chosen from the remaining. The total number of aggregates is then
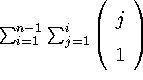. After simplification this becomes
. For example, when n = 10, this number is
165, a great reduction from 
. The savings are even more
significant for n = 20, where this number is 1330, much smaller than
.
The base cube is n-dimensional. As intermediate aggregates are calculated by traversing the lattice (converted into a DAG by the left schedule) up from level n, the following happens: 1) Dimensionality decreases at each level, 2) number of aggregates increase and 3) sizes of each aggregate decrease.